Volume d'une boite

Problème

D'un carré de carton de 10 cm de côté, on enlève dans chaque coin un petit carré de x cm de côté afin de réaliser le patron d'une boîte parallélépipédique sans couvercle. On note V(x) le volume en \(cm^3\) de la boîte ainsi obtenue.
On souhaite trouver, à 1 mm près, la valeur de x pour laquelle la boite a le plus grand volume possible.

Dans l'animation ci-dessous, le point bleu peut être déplacé.

Partie A : Construction du patron avec Python

On souhaite dans un premier temps construire à l'aide du module turtle de Python le programme qui permet lorsque son utilisateur saisie une valeur de x d'obtenir le dessin du patron de la boite correspondante.
Pour cela, on prendra comme unité : 1mm=1px.

On pourra utiliser l'aide suivante dans laquelle les principales structures algorithmiques sont programmées en Python et en Scratch. En Python le symbole # devant une ligne permet d'écrire un commentaire qui ne sera pas lu par Python. Veillez à respecter l'indentation de votre code à l'aide de la touche Tabulation du clacier ou de 4 espaces.

Python	Scratch
#Pour affecter 5 à la variable i : i=5
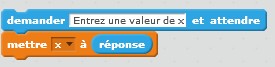
#Pour permettre la saisie d'une chaîne de caractères : x=input('Entrez une valeur de x\n')
#Pour convertir la chaîne de caractère x en un entier n : n=int(x) #Pour convertir la chaîne de caractère x en ... #... un float f (un nombre réel f) f=float(x)	Cela se fait automatiquement en Scratch
Boucle bornée
#Lorsqu'on veut répéter 4 fois une suite d'instructions : for i in range(4): Instructions
Boucle non bornée
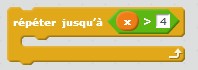
#Lorsqu'on veut répéter une suite d'instructions... #... tant que x est inférieur ou égal à 4 : while x<=4: Instructions
Structure conditionnelle
if condition: Instruction si vrai else: Instruction si faux

Construction d'un document synthèse

Dans un fichier OpenOffice, copiez votre code Python puis construisez un tableau dans lequel, figureront 5 patrons correspondant à 5 valeurs de x différentes. On prendra soin d'indiquer les différentes valeurs de x.Correction

Partie B : Le calcul de volume

On veut maintenant construire un nouveau programme qui permet à son utilisateur d'obtenir le volume de la boite lorsque celui-ci saisie une valeur de x.
Pour cela, appropriez vous le code ci-dessous qui décrit la création d'une fonction sous Python.
La fonction construite sera appelée Volume.

#Création de la fonction qui permet de multiplier deux nombres :

def multiplication(a,b):
	return a*b

#Utilisation de la fonction :

multiplication(2,3)
		

Travail 1

Dans le tableau de votre document de synthèse, ajoutez une colonne dans laquelle vous indiquerez les volumes des 5 boites, obtenus pour les 5 valeurs de x choisies dans la partie A. Imprimez puis collez cette feuille.

Travail 2

Sur une feuille de papier millimétré, construisez le nuage de points de pas 1mm de la fonction Volume. Collez cette feuille puis répondez au problème posé en début d'activité.

Partie C : Un nuage de points pour répondre graphiquement au problème posé

Appropriez vous le code ci-dessous en commentant chacune des instructions.

	 
from pylab import *
			
#représentation du point de coordonnées (3;2)
xlabel("axe des abscisses")
ylabel("axe des ordonnées")
xlim(0, 6)
ylim(0, 5)
plot(2,3,'ro')
show()
		

En utilisant le Code 2, modifiez votre programme, de manière à afficher le nuage de points, de pas 1 mm, de la fonction Volume. On rappelle l'échelle : 1 mm = 1px.

Pour cela on utilisera successivement les deux méthodes suivantes :

Méthode 1 En utilisant une structure Pour (on commencera par compter le nombre de points à dessiner).

Méthode 2 En utilisant une structure Tant Que.

Travail 3

Copiez les deux codes précédents ainsi que le nuage de points obtenu sur une page OpenOffice puis imprimez et collez le document ainsi créé.

Partie D : Programme de la recherche de l'approximation du volume maximal

Dans cette partie, nous souhaitons construire un programme qui va nous permettre d'obtenir, au millimètre près, la valeur de x pour laquelle le volume est maximal ainsi que la valeur du volume correspondant.

1. Cherchez un algorithme permettant de répondre à ce problème puis mettez le en forme.
2. Programmer cet algorithme à l'aide de Python.

Travail 4

Sur un document OpenOffice, copiez le code Python construit pour répondre au problème et donnez les valeurs obtenues.
Sont-elles cohérentes graphiquement ?

Partie E : Questions de synthèse

1. Posons a=2,1 et b=3,7. Parmi ces deux valeurs, laquelle choississez-vous de manière à obtenir la boite de plus grand volume ? Justifier.
2. Donner le tableau de variation de la fonction Volume sur [0;5]
3. Donner les extrema de la fonction Volume sur [0;5].
4. Question ouverte : Comment construire un cube ?