Activité 9 : Un premier calcul d'aire sous une courbe

Objectif : Construire un maillage du carré unité et donner une approximation de l'aire sous la courbe représentative de la fonction carrée sur [0;1]

On considère la fonction \(f\) définie sur \(\small{\mathbb{R}}\) par \(f(x)=x^2\) et soit \(C_f\) sa courbe représentative.

1. Créer un programme avec Python qui permette à son utilisateur de dessiner un maillage du carré unité dont l'écart entre les mailles sera défini par l'utilisateur.

   

   Aide à la programmation : Voici un morceau de code qui permet de dessiner un nuage de points.
   

   #Importation du module pylab qui permet de dessiner dans un repère
   #http://www.courspython.com/introduction-courbes.html
   from pylab import*
   
   #Création d'un nuage de points
   xlabel("légende des abscisses ")   #Légende sur l'axe des abscisses
   ylabel("légende des ordonnées ")   #Légende sur l'axe des abscisses
   xlim(0, 4.5)              #xmin=0 et xmax=5
   ylim(0, 3.5)              #ymin=0 et ymax=100
   for i in range(4):
       x=[1,2,3,4]        # liste des abscisses des points
       y=[0,1,2,3]               # liste des ordonnées des points
       plot(x,y,'ro')    # représentation du point de coordonnées (p*i,y)
   show()

2. Colorer en rouge les points qui se trouvent sous \(C_f\) et en bleu les points qui se trouvent au dessus de \(C_f\) comme le montre la figure ci-dessous.
   

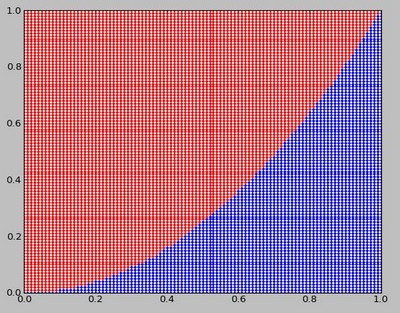
3. Compter les points qui se trouvent sous la courbe \(C_f\), puis en déduire une approximation de l'aire A.
   

Une solution de cette question : Voir