Activité : Algorithme du PageRank

En plus de l'indexation, les moteurs de recherche utilisent l'architecture du Web pour extraire les pages les plus intéressantes, celles que tout le monde finira par voir parce que les liens mènent à elles. On schématise la « Toile » par un graphe formé de sommets, « les sites », et de flèches, « les liens hypertextes » qui mènent d'un site à l'autre.

Le PageRank ou PR est l'algorithme d'analyse des liens concourant au système de classement des pages Web utilisé par le moteur de recherche Google. Il mesure quantitativement la popularité d'une page web. Le PageRank n'est qu'un indicateur parmi d'autres dans l'algorithme qui permet de classer les pages du Web dans les résultats de recherche de Google (voir en fin de document). Ce système a été inventé par Larry Page, cofondateur de Google

Sans plus d'informations, dans ce qui suit, on va imaginer que l'internaute se déplace au hasard et de manière uniforme (équiprobable). Si trois liens sont présents sur un site, l'internaute utilisera l'un de ces trois liens, avec une chance sur trois pour chacun par exemple.

Exercice 1 : (Avec un dé ou une calculatrice)

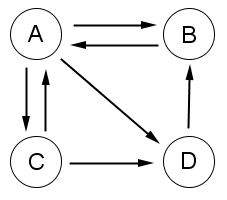
  1. On modélise une portion du Web par le graphe ci-contre.

    On choisit au hasard un point de départ puis on se déplace dans ce graphe, toujours au hasard, durant 5 minutes en notant les différentes pages rencontrées.

    Pour simuler le hasard, on utilisera un dé à 6 faces ou une calculatrice.

  2. Recueillir les sites d'arrivée de chacun des élèves de la classe au bout des 5 minutes.
  3. Compter le nombre de passages sur chaque site et remplir le premier tableau ci-dessous.
 PageRank Graph1

Bilan des déplacements de l'élève :
PageRank tableau

Bilan des déplacements de tous les élèves de la classe :
PageRank tableau
Que constate-t-on ? Quel est le site le plus « attirant » ?

Exercice 2 : (Simulation à l'aide de Python)

  1. En utilisant la fonction Python hasard(...) ci-dessous, qui simule un déplacement d'un internaute dans la portion de Web de l'exercice 1, créer un programme qui effectue 10 déplacements sur la « toile » et affiche les pages visitées.

    Indications : On pourra, par exemple, utiliser une liste Python et les instructions suivantes.

    liste=[] # Déclaration d'une liste Python
    liste.append(x) # Ajoute l'élément x à la fin de l liste1
    liste.count(x) # Renvoie le nombre d'occurrences de x
     
    
from random import*

def hasard(PagePrec):
    if PagePrec=="A":
        choix=choice(["B","C","D"])
    if PagePrec=="B":
        choix="A"
    if PagePrec=="C":
        choix=choice(["A","D"])
    if PagePrec=="D":
        choix="B"
    return choix
    		PageRank Graph1

  2. Modifier le programme précédent de manière à ce que son utilisateur puisse saisir le nombre de déplacements qu'il souhaite et obtienne le site le plus « attirant », c'est à dire le plus fréquemment visité.

Exercice 3 : (Pour aller plus loin)

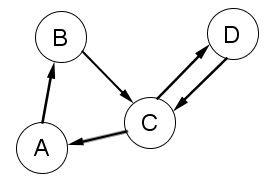
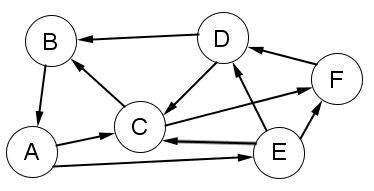
Dans les deux configurations suivantes, modifier le programme précédent de manière à ce qu'il trouve le site le plus « attirant ».

PageRank Graph2
PageRank Graph3
Graphe 2
Graphe 3

Remarque : On peut aussi utiliser le simulateur de graphe Gephi ( https://gephi.org/ ). Il permet de calculer le PageRank de chaque page.

Plus généralement : Selon le brevet Google, les critères de classement des pages sont  :