Page 14

Page Précédente
Sommaire

Python dans le cours de Sciences Physiques

Les nouveaux programmes de sciences physiques (appliquables en septembre 2019), recommandent de faire des liens avec les sciences numériques à l'aide de programmations et de simulations (programme de Sciences physique de seconde).
Le langage de programmation conseillé est le langage Python.

    Dans ce qui suit, vous trouverez :
  1. Des codes de bases en Python qui permettent de démarrer dans les domaines abordés par les programmes.
  2. Quelques exemples de codes dont on pourra s'inspirer pour construire des activités pour la seconde et la première.

Des codes de bases pour démarrer

Dans ce paragraphe, on trouvera des liens sur des codes de bases, qui permettront d'apprendre très rapidement :

Pour la classe de seconde

Activité : Caractéristique d'un dipole

Capacités numériques : Représenter un nuage de points associé à la caractéristique d'un dipôle et modéliser la caractéristique de ce dipôle à l'aide de Python.

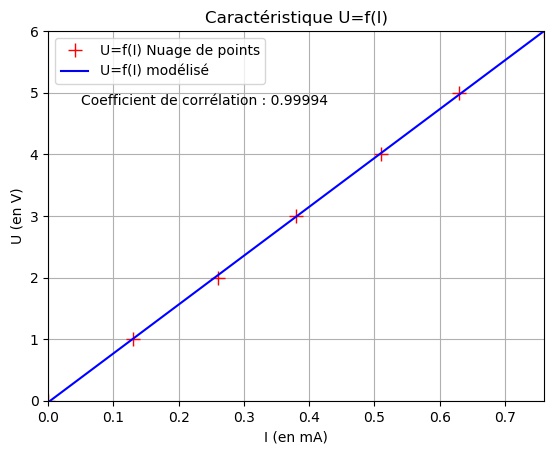
Le code Python qui est présenté dans cette activité permet de représenter et de modéliser la caractéristique tension-courant U=f(I) d'une photorésistance.
Le tableau de valeurs suivant a été rempli de manière expérimentale.
Données Dipôle
Copiez le code suivant dans l'éditeur EduPython. Analysez le puis lancez le programme en observant ce qu'il produit dans la console et la fenêtre graphique.

	
# -*- coding: utf-8 -*-
# ====================================================================
# Programme permettant de représenter et de modéliser
# la caractéristique U=f(I) d'une photorésistance
# ====================================================================


# La bibliothèque NumPy (http://www.numpy.org/) permet d'effectuer des calculs
# numériques avec Python.
# Pour en savoir plus :
# https://www.courspython.com/apprendre-numpy.html
from numpy import*

#Importation de la bibliothèque matplotlib.pyplot (tracer de courbe)
#http://www.python-simple.com/python-matplotlib/pyplot.php
#https://matplotlib.org/users/pyplot_tutorial.html
from matplotlib.pyplot import*

# Définition de 2 listes pour les 2 variables U et I
U=[0.0,1.0,2.0,3.0,4.0,5.0,6.0]        # U (en V)
I=[0.00,0.13,0.26,0.38,0.51,0.63,0.76] # I (en mA)

# Affichage du nuage de points de coordonnées (I,U): U=f(I)
figure("Etude d'une photorésistance")  # Nom de la fenêtre contenant la figure
title('Caractéristique U=f(I)')        # Titre du graphique
xlabel('I (en mA)')                    # Légende axe des abscisses
ylabel('U (en V)')                     # Légende axe des ordoonnées
axis([min(I),max(I),min(U),max(U)])    # Min et max des axes
plot(I,U,'r+',ms=10,label='U=f(I))# Trace le nuage de points')
                                           # '+' rouge de taille 10


#Calcul du coefficient de corrélation (arrondit à 5 chiffres)
# et affichage dans la figure
txt='Coefficient de corrélation : {}'.format(round(corrcoef(I,U)[0][1],5))
text(0.05,4.8,txt)  #Affichage de tx en (0,05;4,8)


# Modélisation du nuage de points par la droite d'équation U_mod=a*I+b

# Calcule les coefficients de la droite modélisant le nuage
# de points et les range dans un tableau nommé Modele
# pour en savoir plus :
# http://www.python-simple.com/python-numpy-scipy/fitting-regression.php
Modele = polyfit(I,U,1)

# Affecte les coefficients du modèle aux variables a et b
# version du livre : a,b = [coef for coef in Modele]

# Ma simplification :
a=Modele[0]
b=Modele[1]


# Pour chaque valeur i de l'intensité, calcule l'ordonnée donnée par
# la modélisation et range les ordonnées dans une liste appelée U_mod
# version du livre : U_mod = [a*i+b for i in I]

# Ma simplification :
U_mod=[]
for i in I:
    U_mod.append(a*i+b)


# Trace les points de coordonnées I et U_mod en bleu et reliés
plot(I,U_mod,'b-',label='U=f(I) modélisé')

# Affiche l'équation de la droite en arrondissant les coefficients a et b
# à 1 chiffre après la virgule et en précisant les unités de I et U
print('Expression du modèle')
if (round(b,1)==0.0):
    print('fonction linéaire : U (en V) = ',round(a,1),'x I (en mA)')
else:
    print('fonction affine : U (en V)=',round(a,1),'x I (en mA) +(',round(b,1),')')

savefig('CaractDipole.jpg', bbox_inches='tight')

grid()                         # Affiche une grille
legend()                       # Affiche la légende
show()                         # Affiche la figure
Caractéristique Dipôle

On remarquera que le coefficient de corrélation a été calculé et inséré dans le graphique.

Activité : Positions successives d'un système, mouvement et vecteur vitesse

Capacités numériques :

On étudie le mouvement d'une balle de golf à partir d'une chronophotographie dans le but de tracer les vecteurs vitesses au cours du temps.
Les positions relevées toutes les 0,066 s sont rassemblées dans un tableau. On remarquera que ces données pourraient être extraites d'un fichier cvs.

Golf

Le code suivant produit l'image ci-dessous. 

	
# -*- coding: utf-8 -*-

from matplotlib.pyplot import*

#Création du tableau des valeurs du temps
t=[]
for i in range(11):
    t.append(i*0.066)
x=[0.01,0.25,0.57,0.91,1.22,1.54,1.87,2.16,2.49,2.81,3.15]
y=[0.01549,0.3404,0.6812,1.010,1.297,1.559,1.768,1.95,2.08,2.158,2.193]
plot(x,y,'ro',label="y=f(x)")
xlabel("x")
ylabel("y")
grid()
legend()
title("Trajectoire de la balle")
show()
Caractéristique Dipôle

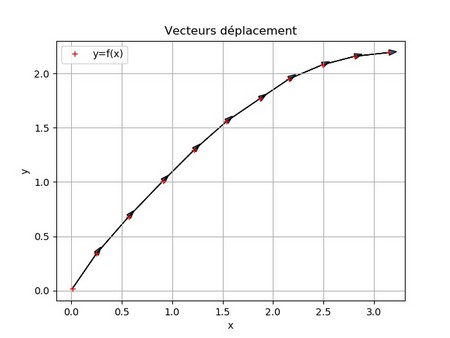
On souhaite à présent représenter les vecteurs déplacements.
Il faut redimensionner la liste des valeurs pour qu'elle contienne un élément de moins car on ne peut pas calculer x[i+1] et y[i+1] pour la dernière valeur de i.
On rappelle que la fonction len(...) permet de connaitre la taille d'une liste. 

	
# -*- coding: utf-8 -*-

#from numpy import*
from matplotlib.pyplot import*

#Création du tableau des valeurs du temps
t=[]
for i in range(11):
    t.append(i*0.066)
x=[0.01,0.25,0.57,0.91,1.22,1.54,1.87,2.16,2.49,2.81,3.15]
y=[0.01549,0.3404,0.6812,1.010,1.297,1.559,1.768,1.95,2.08,2.158,2.193]
plot(x,y,'r+',label="y=f(x)")

#On enlève la dernière valeur
n=len(t)-1
#on fait tracer une série de vecteurs
for i in range(n) :
    arrow(x[i],y[i],x[i+1]-x[i],y[i+1]-y[i],head_width=0.05)
# de position initiale x[i],y[i], de coordonnées x[i+1]-x[i] et y[i+1]-y[i]
# head_width est la largeur de la tête

xlabel("x")
ylabel("y")
grid()
legend()
title("Vecteurs déplacement")
savefig('Golf_Vecteur_Deplacement.jpg')
show()
Vecteur Déplacement

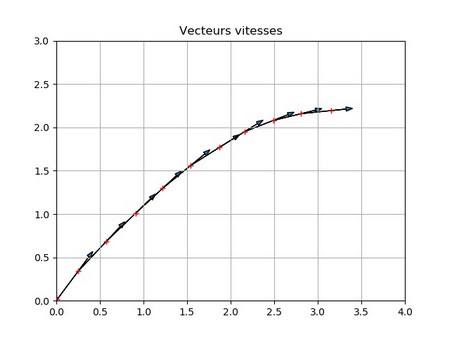
On souhaite à présent représenter les vecteurs vitesses.
On rappelle que \( \vec{V_i}=\frac{\vec{M_{i}M_{i+1}}}{t_{i+1}-t_i}\). On ne peut donc pas dessiner le vecteur vitesse du dernier point de la liste. Il faut en tenir compte dans le code et le dessin suivant.
On remarquera également que les lignes 12 et 13 auraient du être écrites sur la même ligne. 

	
# -*- coding: utf-8 -*-

from matplotlib.pyplot import*

#Création du tableau des valeurs du temps
t=[]
for i in range(11):
    t.append(i*0.066)
x=[0.01,0.25,0.57,0.91,1.22,1.54,1.87,2.16,2.49,2.81,3.15]
y=[0.01549,0.3404,0.6812,1.010,1.297,1.559,1.768,1.95,2.08,2.158,2.193]
plot(x,y,'r+',label="y=f(x)")

m=len(t)-1
for i in range(m) :
    arrow(x[i],y[i],0.1*(x[i+1]-x[i])/(t[i+1]-t[i]),
    0.1*(y[i+1]-y[i])/(t[i+1]-t[i]),head_width=0.05)
# on multiplie par 0.1 pour que la figure soit lisible.
xlim(0,4)
ylim(0,3)
grid()

title("Vecteurs vitesses")
savefig('Golf_Vecteur_Vitesse.jpg')
show()
Vecteur Vitesse
Page Précédente
Sommaire


Page 14